ਅਨੰਤ ਸਰੋਤ : ਪੰਜਾਬੀ ਸਭਿਆਚਾਰ ਸ਼ਬਦਾਵਲੀ ਕੋਸ਼, ਪਬਲੀਕੇਸ਼ਨ ਬਿਊਰੋ, ਪੰਜਾਬੀ ਯੂਨੀਵਰਸਿਟੀ, ਪਟਿਆਲਾ।

ਅਨੰਤ (ਨਾਂ,ਪੁ) ਸੱਜੀ ਬਾਂਹ ’ਤੇ ਪਾਉਣ ਵਾਲਾ ਬਾਰਾਂ ਗੰਢਾਂ ਦੀ ਸ਼ਕਲ ਦਾ ਗਹਿਣਾ

ਅਨੰਤ ਸਰੋਤ : ਗੁਰੁਸ਼ਬਦ ਰਤਨਾਕਾਰ ਮਹਾਨ ਕੋਸ਼, ਪਬਲੀਕੇਸ਼ਨ ਬਿਊਰੋ, ਪੰਜਾਬੀ ਯੂਨੀਵਰਸਿਟੀ, ਪਟਿਆਲਾ।

ਅਨੰਤ. ਵਿ—ਬਿਨਾ ਅੰਤ. ਬੇਅੰਤ. ਅਨੇਕ. ਨਾਨਾ. “ਇਕਸੁ ਤੇ ਹੋਇਓ ਅਨੰਤਾ.” (ਮਾਝ ਅ: ਮ: ੫) ੨ ਸੰਗ੍ਯਾ—ਕਰਤਾਰ. ਵਾਹਗੁਰੂ। ੩ ਆਕਾਸ਼। ੪ ਸ਼ੇ੄ਨਾਗ। ੫ ਬਲਭਦ੍ਰ. ਇਹ ਸ਼ੇ੄ ਦਾ ਅਵਤਾਰ ਮੰਨਿਆ ਹੈ, ਇਸ ਲਈ ਨਾਂਉ ਅਨੰਤ ਹੈ. “ਅਨੰਤ ਕੇ ਊਪਰ ਕੋਪ ਚਲਾਯੋ.” (ਕ੍ਰਿਸਨਾਵ) ੬ ਭੁਜਾ ਉੱਪਰ ਪਹਿਰਣ ਦਾ ਇੱਕ ਗਹਿਣਾ , ਜਿਸ ਨੂੰ ਸ਼ੇ੄ਨਾਗ ਦੀ ਮੂਰਤੀ ਕਲਪਕੇ ਹਿੰਦੂ ਭਾਦੋਂ ਸੁਦੀ ੧੪ ਨੂੰ ਪਹਿਰਦੇ ਹਨ. ਦੇਖੋ, ਅਨੰਤ ਚੌਦੇ.

ਅਨੰਤ ਸਰੋਤ : ਪੰਜਾਬੀ ਵਿਸ਼ਵ ਕੋਸ਼–ਜਿਲਦ ਪਹਿਲੀ, ਭਾਸ਼ਾ ਵਿਭਾਗ ਪੰਜਾਬ

ਅਨੰਤ (Infinity) : ਇਨਫ਼ਿਨਿਟੀ ਸ਼ਬਦ ਲਾਤੀਨੀ ਭਾਸ਼ਾ ਦੇ ‘ਇਨ’ (ਅਨ) ਅਤੇ ‘ਫ਼ਿਨਿਸ’ (ਅੰਤ) ਦੀ ਸੰਧੀ ਹੈ। ਇਹ ਸ਼ਬਦ ਉਨ੍ਹਾਂ ਰਕਮਾਂ ਲਈ ਵਰਤਿਆ ਜਾਂਦਾ ਹੈ ਜਿਨ੍ਹਾਂ ਦੀ ਗਿਣਤੀ ਜਾਂ ਮਿਣਤੀ ਸੀਮਤ ਨਹੀਂ। ਮਿਸਾਲ ਲਈ ਅਸੀਮ ਸਰਲ ਰੇਖਾ ਦੀ ਲੰਬਾਈ ਅਨੰਤ ਹੈ।

          ਗਣਿਤ ਵਿਚ ‘ਅਨੰਤ’ ਨੂੰ ∞ ਚਿੰਨ੍ਹ ਨਾਲ ਦਰਸਾਉਂਦੇ ਹਨ। ਅਨੰਤ ਦੀ ਵਿਆਖਿਆ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਹੈ :

          ਫਰਜ਼ ਕਰੋ ਕਿ x ਕੋਈ ਚੱਲ (variable) ਹੈ ਅਤੇ f(x) ਇਸ ਦਾ ਕੋਈ ਫਲਨ (function) ਹੈ। ਜੇ x ਕਿਸੇ ਸੰਖਿਆ a ਵੱਲ ਵਧੇ ਤਦ f (x) ਇਸ ਤਰ੍ਹਾਂ ਵੱਧਦਾ ਹੀ ਚਲਿਆ ਜਾਏਗਾ ਕਿ ਉਹ ਦਿੱਤੀ ਹੋਈ ਹਰ ਸੰਖਿਆ G ਤੋਂ ਵੱਡਾ ਹੋ ਜਾਏ ਅਤੇ ਵੱਡਾ ਹੀ ਰਹੇ, ਚਾਹੇ G ਕਿੰਨਾ ਹੀ ਵੱਡਾ ਹੋਵੇ। ਸੋ ਕਿਹਾ ਜਾਂਦਾ ਹੈ x→a ਲਈ f(x) ਦੀ ਸੀਮਾ ਅਨੰਤ ਹੈ। ਜੇ x ਦਾ ਮੁੱਲ ਕਿਸੇ ਸੰਖਿਆ ‘a’ ਦੇ ਨੇੜੇ ਲਿਜਾਉਣ ਨਾਲ f(x) ਦਾ ਮੁੱਲ ਇਸ ਤਰ੍ਹਾਂ ਵੱਧਦਾ ਚਲਾ ਜਾਵੇ ਕਿ ਇਹ ਮੁੱਲ ਹਮੇਸ਼ਾਂ ਕਿਸੇ ਦਿੱਤੀ ਹੋਈ ਸੰਖਿਆ G ਤੋਂ ਵੱਡਾ ਰਹੇ, ਚਾਹੇ G ਕਿੰਨਾ ਹੀ ਵੱਡਾ ਕਿਉਂ ਨਾ ਹੋਵੇ ਤਾਂ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ x ਨੂੰ ‘a’ ਤਕ ਲਿਜਾਉਣ ਲਈ (x→a), f(x) ਦੀ ਸੀਮਾ ਅਨੰਤ (∞) ਹੈ।

          ਭਿੰਨਾਂ ਦੀ ਪਰਿਭਾਸ਼ਾ ਤੋਂ ਸਪਸ਼ਟ ਹੈ ਕਿ ਭਿੰਨ a/b ਉਹ ਸੰਖਿਆ ਹੈ ਜਿਸ ਨੂੰ b ਨਾਲ ਗੁਣਾ ਕਰਨ ਤੇ ਗੁਣਨਫਲ a ਪਰਾਪਤ ਹੁੰਦਾ ਹੈ। ਜੇ a, b ਵਿਚੋਂ ਕੋਈ ਵੀ ਸਿਫ਼ਰ (zero) ਨਹੀਂ ਤਾਂ a/b ਇਕ ਅਜੇਹੀ ਰਕਮ ਨੂੰ ਸਪਸ਼ਟ ਕਰਦਾ ਹੈ ਜਿਸ ਦੇ ਬਰਾਬਰ ਕੋਈ ਦੂਜੀ ਰਕਮ ਨਹੀਂ। ਇਸ ਤੋਂ ਸਪੱਸ਼ਟ ਹੈ ਕਿ o/b ਦਾ ਮੁੱਲ ਸਦਾ ਬਰਾਬਰ ਰਹਿੰਦਾ ਹੈ, ਚਾਹੇ b ਕੋਈ ਵੀ ਸੀਮਿਤ ਸੰਖਿਆ (finite number) ਹੋਵੇ। ਇਸ ਨੂੰ ਰੈਸ਼ਨਲ ਸੰਖਿਆਵਾਂ (rational numbers) ਦੀ ਸਿਫਰ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਾਰਡੀਨਲ (cardinal number) ਸੰਖਿਆ 0 ਦੇ ਬਰਾਬਰ ਹੈ। ਇਸ ਦੇ ਉਲਟ b/o ਇਕ ਅਰਥਹੀਨ ਪਦ ਹੈ ਜਿਸ ਨੂੰ ਅਨੰਤ ਸਮਝਣਾ ਭੁੱਲ ਹੈ। ਜੇ a/b ਵਿਚ a ਸਥਿਰ ਰਹਿੰਦਾ ਹੈ, b ਘਟਦਾ ਜਾਂਦਾ ਹੈ ਅਤੇ a, b ਦੋਵੇਂ ਧਨ (positive) ਹਨ ਤਾਂ a/b ਦੀ ਕੀਮਤ ਵੱਧਦੀ ਜਾਵੇਗੀ। ਜੇ b ਦਾ ਮੁੱਲ ਸਿਫ਼ਰ ਵਲ ਨੂੰ ਸਰਕਦਾ ਹੈ ਤਾਂ ਅੰਤ ਵਿਚ a/b ਹਰ ਵੱਡੀ ਤੋਂ ਵੱਡੀ ਸੰਖਿਆ ਨਾਲੋਂ ਵੱਧ ਜਾਵੇਗਾ। ਇਸ ਗੱਲ ਨੂੰ ਅਸੀਂ ਹੇਠ ਲਿਖੇ ਅਨੁਸਾਰ ਦਰਸਾਉਂਦੇ ਹਾਂ :

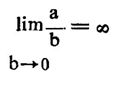
ਇਸ ਸਿੱਟੇ ਦੇ ਆਧਾਰ ਤੇ ਅਵਿਗਿਆਨਕ ਢੰਗ ਨਾਲ ਕਿਹਾ ਜਾਂਦਾ ਹੈ ਕਿ

          ਜਾਰਜ ਕੈਂਟਰ (George Cantor ; 1845-1918) ਨੇ ਅਨੰਤ ਦੀ ਸਮੱਸਿਆ ਨੂੰ ਇਕ ਹੋਰ ਢੰਗ ਨਾਲ ਸਮਝਾਇਆ ਹੈ। ਕੈਂਟਰ ਸੰਖਿਆਵਾਂ, ਜੋ ਟ੍ਰਾਂਸਫ਼ਿਨਿਟ ਸੰਖਿਆਵਾਂ (transfinite numbers) ਵੀ ਆਖੀਆਂ ਜਾਂਦੀਆਂ ਹਨ, ਜੁਮੈਟਰੀ (Geometry) ਤੇ ਸੀਮਾ-ਸਿਧਾਂਤ (Limit theorem) ਵਿਚ ਅਨੰਤ ਦੀ ਪ੍ਰਚਲਤ ਪਰਿਭਾਸ਼ਾ ਨਾਲੋਂ ਵੱਖਰੀ ਕਿਸਮ ਦੀਆਂ ਹਨ। ਕੈਂਟਰ ਨੇ ਛੋਟੀ ਤੋਂ ਛੋਟੀ ਟ੍ਰਾਂਸਫ਼ਿਨਿਟ ਕਾਰਡੀਨਲ ਸੰਖਿਆ (transfinite cardinal number) A­_o (ਅਕਾਰ ਸਿਫ਼ਰ, ਅਲਫ਼-ਜ਼ੀਰੋ) ਦੀ ਵਿਆਖਿਆ ਪ੍ਰਾਕ੍ਰਿਤਕ ਸੰਖਿਆਵਾਂ 1,2,3 ....ਦੇ ਸੈੱਟ ਦੇ ਕਾਰਡੀਨਲ ਨੰਬਰਾਂ ਨਾਲ ਕੀਤੀ ਹੈ। ਇਹ ਸਾਬਤ ਹੋ ਚੁੱਕਾ ਹੈ ਕਿ A_o+n=A_o ਜਿਸ ਵਿਚ n ਕੋਈ ਨਿਸ਼ਚਿਤ (definite) ਪੂਰਨ ਅੰਕ (integral number) ਹੈ। ਕੈਂਟਰ ਨੇ ਸਿਰਫ਼ A_o ਦੇ ਹੀ ਨਹੀਂ, ਸਗੋਂ ਕਈ ਐਲਫ਼ਾ ਸੰਖਿਆਵਾਂ A_o, A₁,…… ਦੇ ਸਿਧਾਂਤ ਦਾ ਵੀ ਵਿਕਾਸ ਕੀਤਾ ਹੈ। ਹਾਰਡੀ (Hardy) ਨੇ ਕਾਰਡੀਨਲ ਸੰਖਿਆ A₁ ਵਾਲੇ ਬਿੰਦੂਆਂ ਦੇ ਸੈੱਟ ਬਣਾਉਣ ਲਈ ਤਰੀਕਾ ਦੱਸਿਆ ਹੈ। ਸੰਖਿਆ M(=<A_o) ਕਾਂਟੀਨੀਊਮ (continuum) ਦੀ ਅਰਥਾਤ ਵਾਸਤਵਿਕ ਸੰਖਿਆਵਾਂ ਦੇ ਸੈੱਟ ਦੀ ਕਾਰਡੀਨਲ ਸੰਖਿਆ ਹੈ। ਇਕ ਤੋਂ ਇਕ ਸੰਗਤੀ (one to one correspondence) ਰਾਹੀਂ ਇਹ ਸਾਬਤ ਕੀਤਾ ਜਾ ਸਕਦਾ ਹੈ ਕਿ (0, 1) ਇੰਟਰਵਲ ਵਿਚ ਵੀ ਬਿੰਦੂਆਂ ਦੇ ਸੈੱਟ ਦੀ ਕਾਰਡੀਨਲ ਸੰਖਿਆ M ਹੁੰਦੀ ਹੈ।

          ਵਾਸਤਵਿਕ ਸੰਖਿਆਵਾਂ, 1,2,3,…..ਦੇ ਸੈੱਟ ਨਾਲ ਜੁੜੀ ਹੋਈ ਟ੍ਰਾਂਸਫ਼ਿਨਿਟ ਆਰਡੀਨਲ ਸੰਖਿਆ (transfinite ordinal number) ਨੂੰ 𝛚 (omega) ਲਿਖਦੇ ਹਨ ਅਤੇ ਇਸ ਨੂੰ ਪਹਿਲੀ ਟ੍ਰਾਂਸਫ਼ਿਨਿਟ ਆਰਡੀਨਲ ਸੰਖਿਆ ਕਹਿੰਦੇ ਹਨ। ਕਿਸੇ ਦਿੱਤੇ ਹੋਏ ਇੰਟਰਵਲ (a, b) ਵਿਚ p₁, p₂, P₃,…….ਬਿੰਦੂਆਂ ਦੇ ਇਕ ਅਨੁਕ੍ਰਮ (sequence) ਉਤੇ ਜੋ ਵੱਧਣ ਵਾਲੀਆਂ ਸੰਖਿਆਵਾਂ b₁, b₂, b₃, ਦੇ ਅਨੁਕ੍ਰਮ ਨੂੰ ਸਪਸ਼ਟ ਕਰਦਾ ਹੈ, ਵਿਚਾਰ ਕਰੋ :

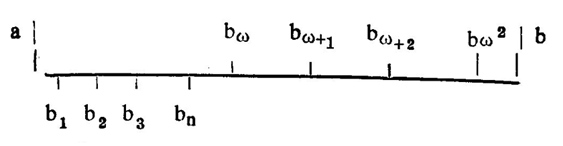
          ਇਸ ਅਨੁਕ੍ਰਮ ਦਾ ਕੋਈ ਸੀਮਾ-ਬਿੰਦੂ (limiting point) ਹੋਵੇਗਾ ਜੋ ਇਨ੍ਹਾਂ ਸਾਰਿਆਂ ਬਿੰਦੂਆਂ ਦੇ ਸੱਜੇ ਪਾਸੇ ਹੋਵੇਗਾ, ਇਸ ਨੂੰ ਅਸੀ b_𝛚 ਰਾਹੀਂ ਦਰਸਾ ਸਕਦੇ ਹਾਂ। ਫਰਜ਼ ਕਰੋ ਕਿ ਬਿੰਦੂ b_𝛚 ਦੇ ਉਪਰੰਤ ਕਈ ਹੋਰ ਬਿੰਦੂ ਅਜਿਹੇ ਵੀ ਹਨ ਜਿਨ੍ਹਾਂ ਨੂੰ ਅਸੀਂ b₁……, b₂……, b_n….., b_𝛚 . ਵਾਲੇ ਸੈੱਟ ਨਾਲ ਜੁੜੇ ਹੋਏ ਮੰਨਾਂਗੇ। ਫਿਰ ਇਨ੍ਹਾਂ ਬਿੰਦੂਆਂ ਨੂੰ ਅਸੀਂ b_𝛚+1, b_𝛚+2, …. ਰਾਹੀਂ ਸਪੱਸ਼ਟ ਕਰਾਂਗੇ। ਜੇ b_𝛚, b_𝛚+1, b_𝛚+2, … ਨਾਂ ਵਾਲਿਆਂ ਬਿੰਦੂਆਂ ਦੇ ਸੈੱਟ ਦਾ ਕੋਈ ਅੰਤਮ ਬਿੰਦੂ ਨਾ ਹੋਵੇ ਅਤੇ ਇਹ ਸਭ (a,b) ਦੇ ਇੰਟਰਵਲ ਅੰਦਰ ਸਥਿਤ ਹੋਣ ਤਾਂ ਇਹ ਸੈੱਟ ਦਾ ਜੋ ਸੀਮਾ-ਬਿੰਦੂ ਹੋਵੇਗਾ ਉਸ ਨੂੰ ਅਸੀਂ b_𝛚² ਦੁਆਰਾ ਸਪੱਸ਼ਟ ਕਰ ਸਕਦੇ ਹਾਂ, ਇਸ ਲਈ ਸਾਨੂੰ ਕ੍ਰਮ ਸੰਖਿਆਵਾਂ (ordinal numbers)  1, 2, 3, …. _𝛚, _𝛚+1, _𝛚+2,  …. _𝛚2, _𝛚2+1…., _{𝛚3 .}, _𝛚2²……ਪਰਪਾਤ ਹੁੰਦੀਆਂ ਹਨ।

          ਗਣਿਤ ਵਿਸ਼ਲੇਸ਼ਣ ਵਿਚ ਅਸੀਂ ਕਈ ਵਾਰ ਅਨੰਤ ਵਲ ਵੱਧਣ ਵਾਲੇ ਅਨੁਕ੍ਰਮਾਂ ਦੇ ਵਾਧੇ ਦੀ ਤੁਲਨਾ ਕਰਦੇ ਹਾਂ। ਲੰਡਾਊ (Landau) ਨੇ O,o, ~ ਨਾਂ ਵਾਲੀ ਸੰਕੇਤ-ਲਿਪੀ ਪ੍ਰਚਲਤ ਕੀਤੀ ਹੈ, ਜਿਸ ਦੀ ਵਿਆਖਿਆ ਇਉਂ ਹੈ; ਜੇ f(x) ਅਤੇ 𝛟 (x) ਧਨਾਤਮਕ (positive) ਹੋਣ ਅਤੇ ਜੇ ਹਰ ਇਕ x>x_o ਲਈ f(x)/𝛟(x) ਇਕ ਸਥਿਰ ਰਾਸ਼ੀ 1 ਹੋਵੇ ਤਾਂ x ਦੇ ਅਨੰਤ ਵਲ ਵੱਧਣ ਤੇ f(x)=O {𝛟 (x)} ਹੁੰਦਾ ਹੈ। ਜੇ ਹਰ ਇਕ x>x_o ਲਈ f(x)/𝛟(x) <εਹੋਵੇ, ਜਿਸ ਵਿਚ εਕੋਈ ਮੰਨੀ ਹੋਈ ਛੋਟੀ ਸੰਖਿਆ ਹੈ, ਤਾਂ x ਦੇ ਅਨੰਤ ਵਲ ਅੱਗੇ ਵੱਧਣ ਤੇ f(x)=o{𝛟(x)} ਹੁੰਦਾ ਹੈ ਅਤੇ ਜੇ x ਦੇ ਅਨੰਤ ਵੱਲ ਅੱਗੇ ਵੱਧਣ ਤੇ f(x)/𝛟(x)=1 ਅਥਵਾ ਕੋਈ ਹੋਰ ਸੀਮਤ ਸੰਖਿਆ ਹੋਵੇ ਤਾਂ f(x) ~ 𝛟 (x) ਲਿਖਦੇ ਹਾਂ। ਇਸ ਲਈ ਜਦ n→∞ ਤਾਂ n²+20ⁿ+1000~n² ਲਿਖਦੇ ਹਾਂ। ਆਮ ਤੌਰ ਤੇ ਦੋਵੇਂ ਲੜੀਆਂ ਅਨੰਤ ਵਲ ਅੱਗੇ ਵੱਧਦੀਆਂ ਹਨ ਅਤੇ ਇਨ੍ਹਾਂ ਦਾ ਇਹ ਵਾਧਾ ਲਗਭਗ ਬਰਾਬਰ ਰਹਿੰਦਾ ਹੈ।

          ਪਾਲ-ਦੁ ਬੋਇਸ, ਰੀਮਾਨ (Riemann) ਅਤੇ ਜੀ. ਐਚ. ਹਾਰਡੀ ਨੇ ਫਲਨ ਦੇ ਤਰੀਕਿਆਂ ਦੇ ਵਾਧੇ ਵਿਚ ਤੁਲਨਾ ਕਰਨ ਲਈ ਅਨੰਤ ਦੇ ਪੈਮਾਨਿਆਂ (scales of infinity) ਦੀ ਵਿਆਖਿਆ ਕੀਤੀ ਹੈ।

ਅਨੰਤ ਸਰੋਤ : ਪੰਜਾਬੀ ਕੋਸ਼ ਜਿਲਦ ਪਹਿਲੀ (ੳ ਤੋਂ ਕ)

ਅਨੰਤ, ਸੰਸਕ੍ਰਿਤ / ਵਿਸ਼ੇਸ਼ਣ : ਬਿਨਾਂ ਅੰਤ, ਬਿਅੰਤ, ਜਿਸ ਦਾ ਅੰਤ ਨਹੀਂ, ਬੇਹੱਦ, ਅਪਾਰ, ਪਰਮੇਸ਼ਰ ਪੁਲਿੰਗ  : ਇਕ ਗਹਿਣਾ ਜਿਸ ਦੀਆਂ ਗੰਢਾਂ ਹੁੰਦੀਆਂ ਹਨ ਅਤੇ ਲੋਕ ਸੱਜੀ ਬਾਂਹ ਵਿਚ ਪਾਉਂਦੇ ਹਨ